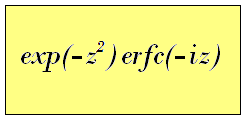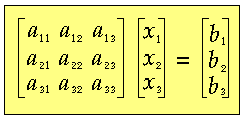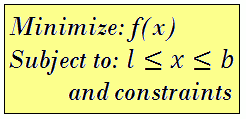NAG Technical Report TR 4/09
Anna Kwiczala
Numerical Algorithms Group, May 2009
Abstract
This report gives detailed instructions on how to call routines in the NAG C and Fortran Libraries from the Octave programming environment.
Contents
Octave [1] is a freely redistributable programming language for numerical computations. It is mostly compatible with MATLAB. The NAG Libraries [2] contain a large selection of numerical and statistical routines, which can be accessed from different languages [3]. This article gives a brief introduction to one of the methods and examples of calling NAG routines from within Octave.
Octave can be extended by dynamically linked functions [4], which are used in the same way as Octave functions. Octave has been written in C++, so it is not surprising that the easiest way of extending it is by writing the linking code in that language. It can be called by Octave directly through its native oct-file interface. Due to the fact that C functions can easily be called from C++, our best choice is to use C++ code together with the NAG C Library.
Octave comes with a ready-made script mkoctfile, which can be used to compile C++ code into oct-files. All we have to do is to write a C++ function calling one of the NAG routines and then use the script. To define the entry point into the dynamically linked function, we need to use the Octave DEFUN_DLD macro in our C++ code. Therefore, our function will look like this:
#include <octave/oct.h>
#include <appropriate NAG header files>
DEFUN_DLD (function_name, args, nargout,
"Function description")
{
octave_value_list retval;
// retrieve input arguments from args
// call NAG routine
// assign output arguments to retval
return retval;
}
where:
- oct.h contains most of the necessary definitions for an oct-file in Octave;
- function_name will be our function's name seen in Octave and it must match the file's name, but be different from any NAG routine names;
- args is the list of arguments to the function of type octave_value_list;
- nargout is the number of output arguments;
- "Function description" is the string that will be seen as the function help text;
- the return type is always octave_value_list.
The rest of the code required will be easier to demonstrate with the use of examples. The code for this article was tested on a Linux machine running 64-bit Fedora 8 (Werewolf) with Octave 3.0.3, plus c++ (GCC) 4.3.3, gcc (GCC) 4.3.3, GNU Fortran (GCC) 4.3.3, Mark 8 of the NAG C Library and Mark 22 of the NAG FORTRAN Library.
3.1 Example 1 Log gamma function ln Γ(x)
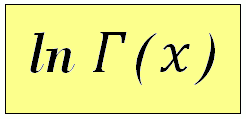 |
The simplest example: we call a function with only one return value - the ln Γ'(x) logarithm gamma function routine nag_log_gamma (s14abc) from the NAG C Library. |
3.2 Example 2 Scaled complex complement of error function, exp(-z2)erfc(-iz)
3.3 Example 3 Approximate solution of complex simultaneous linear equations AX = B
3.4 Example 4 Solving a nonlinear minimization problem
3.5 Example 5 Univariate time series, seasonal and non-seasonal differencing
 |
We call a function from NAG Fortran Library - G13AAF. The function carries out non-seasonal and seasonal differencing on a time series. It returns the differenced values and data which allow the original series to be reconstituted from the differenced series. We use NAG header files [5] for the NAG Fortran Library. |
Octave contains many tools that make extending it fairly easy. The method used in this article is just one of a few possible approaches which we believe is the easiest one. If you want to try different methods, consult Dynamically Linked Functions section on Octave website [4].
- [1] Octave
John W. Eaton
John W. Eaton of University of Wisconsin-Madison, 1998-2006.
http://www.gnu.org/software/octave/index.html - [2] NAG Numerical Libraries
Numerical Algorithms Group
Numerical Algorithms Group Limited, Oxford, UK, 2008.
https://www.nag.com/content/nag-library - [3] Enhancing the Numerical Capability of Your Application
Numerical Algorithms Group
Numerical Algorithms Group Limited, Oxford, UK, 2004.
https://www.nag.com/content/nag-dynamic-link-libraries-dlls - [4] Octave - Dynamically Linked Functions
John W. Eaton
John W. Eaton of University of Wisconsin-Madison, 1996, 1997, 2007.
http://www.gnu.org/software/octave/doc/interpreter/Dynamically-Linked-Functions.html#Dynamically-Linked-Functions
- [5] Calling NAG Fortran Library Routines from C Language Programs Using the NAG C Header Files
Ian Hounam
Numerical Algorithms Group Ltd, Oxford, UK, 2002
https://www.nag.com/content/nag-fortran-library-associated-information#CH
- [6] The NAG C Library
Numerical Algorithms Group Ltd, Oxford, UK, 2009
https://www.nag.com/content/nag-library-c
- [7] The NAG Fortran Library
Numerical Algorithms Group Ltd, Oxford, UK, 2009
https://www.nag.com/content/nag-library-fortran
Copyright 2009 Numerical Algorithms Group