This chapter is concerned with the generation of sequences of independent pseudorandom and quasi-random numbers from various distributions, and models.
 Syntax
Syntax
| C# |
|---|
public static class G05 |
| Visual Basic |
|---|
Public NotInheritable Class G05 |
| Visual C++ |
|---|
public ref class G05 abstract sealed |
| F# |
|---|
[<AbstractClassAttribute>] [<SealedAttribute>] type G05 = class end |
 Background to the Problems
Background to the Problems
 Pseudorandom Numbers
Pseudorandom Numbers
A sequence of pseudorandom numbers is a sequence of numbers generated in some systematic way such that they are independent and statistically indistinguishable from a truly random sequence. A pseudorandom number generator (PRNG) is a mathematical algorithm that, given an initial state, produces a sequence of pseudorandom numbers. A PRNG has several advantages over a true random number generator in that the generated sequence is repeatable, has known mathematical properties and can be implemented without needing any specialist hardware. Many books on statistics and computer science have good introductions to PRNGs, for example Knuth (1981) or Banks (1998).
PRNGs can be split into base generators, and distributional generators. Within the context of this document a base generator is defined as a PRNG that produces a sequence (or stream) of variates (or values) uniformly distributed over the interval . Depending on the algorithm being considered, this interval may be open, closed or half-closed. A distribution generator is a method that takes variates generated from a base generator and transforms them into variates from a specified distribution, for example a uniform, Gaussian (Normal) or gamma distribution.
The period (or cycle length) of a base generator is defined as the maximum number of values that can be generated before the sequence starts to repeat. The initial state of the base generator is often called the seed.
There are six base generators currently available in the NAG Library, these are; a basic linear congruential generator (LCG) (referred to as the NAG basic generator) (see Knuth (1981)), two sets of Wichmann–Hill generators (see Maclaren (1989) and Wichmann and Hill (2006)), the Mersenne Twister (see Matsumoto and Nishimura (1998)), the ACORN generator (see Wikramaratna (1989)) and L'Ecuyer generator (see L'Ecuyer and Simard (2002)).
 NAG Basic Generator
NAG Basic Generator
The NAG basic generator is a linear congruential generator (LCG) and, like all linear congruential generators, has the form:
where the , for , form the required sequence.
The NAG basic generator uses and , which gives a period of approximately .
This generator has been part of the NAG Library since
Mark 6
and as such has been widely used. It suffers from no known problems, other than those due to the lattice structure inherent in all linear congruential generators, and, even though the period is relatively short compared to many of the newer generators, it is sufficiently large for many practical problems.
The performance of the NAG basic generator has been analysed by the Spectral Test, see Section 3.3.4 of Knuth (1981), yielding the following results in the notation of Knuth (1981).
| Upper bound for | ||
The right-hand column gives an upper bound for the values of attainable by any multiplicative congruential generator working modulo .
An informal interpretation of the quantities is that consecutive -tuples are statistically uncorrelated to an accuracy of . This is a theoretical result; in practice the degree of randomness is usually much greater than the above figures might support. More details are given in Knuth (1981), and in the references cited therein.
Note that the achievable accuracy drops rapidly as the number of dimensions increases. This is a property of all multiplicative congruential generators and is the reason why very long periods are needed even for samples of only a few random numbers.
 Wichmann–Hill I Generator
Wichmann–Hill I Generator
This series of Wichmann–Hill base generators (see Maclaren (1989)) use a combination of four linear congruential generators and has the form:
where the , for , form the required sequence. The NAG Library implementation includes 273 sets of parameters, , for , to choose from.
| (1) |
The constants are in the range 112 to 127 and the constants are prime numbers in the range to , which are close to . These constants have been chosen so that each of the resulting 273 generators are essentially independent, all calculations can be carried out in 32-bit integer arithmetic and the generators give good results with the spectral test, see Knuth (1981) and Maclaren (1989). The period of each of these generators would be at least if it were not for common factors between , , and . However, each generator should still have a period of at least . Further discussion of the properties of these generators is given in Maclaren (1989).
 Wichmann–Hill II Generator
Wichmann–Hill II Generator
This Wichmann–Hill base generator (see Wichmann and Hill (2006)) is of the same form as that described in [Wichmann–Hill I Generator], i.e., a combination of four linear congruential generators. In this case , , , , , , , .
Unlike in the original Wichmann–Hill generator, these values are too large to carry out the calculations detailed in (1) using 32-bit integer arithmetic, however, if
then setting
gives
and can be calculated in 32-bit integer arithmetic. Similar expressions exist for , and . The period of this generator is approximately .
Further details of implementing this algorithm and its properties are given in Wichmann and Hill (2006). This paper also gives some useful guidelines on testing PRNGs.
 Mersenne Twister Generator
Mersenne Twister Generator
The Mersenne Twister (see Matsumoto and Nishimura (1998)) is a twisted generalized feedback shift register generator. The algorithm underlying the Mersenne Twister is as follows:
| (i) | Set some arbitrary initial values , each consisting of bits. | ||||
| (ii) | Letting
|
||||
| (iii) | Perform the following operations sequentially:
|
The , for , form the required sequence. The supplied implementation of the Mersenne Twister uses the following values for the algorithmic constants:
where the notation 0xDD indicates the bit pattern of the integer whose hexadecimal representation is DD .
This algorithm has a period length of approximately and has been shown to be uniformly distributed in 623 dimensions (see Matsumoto and Nishimura (1998)).
 ACORN Generator
ACORN Generator
The ACORN generator is a special case of a multiple recursive generator (see Wikramaratna (1989) and Wikramaratna (2007)). The algorithm underlying ACORN is as follows:
| (i) | Choose an integer value . | ||
| (ii) | Choose an integer value , and an integer seed , such that and and are relatively prime. | ||
| (iii) | Choose an arbitrary set of initial integer values, , such that , for all . | ||
| (iv) | Perform the following sequentially:
|
||
| (v) | Set . |
The , for , then form a pseudorandom sequence, with , for all .
Although you can choose any value for , , and the , within the constraints mentioned in (i) to (iii) above, it is recommended that , is chosen to be a large power of two with and is chosen to be odd.
The period of the ACORN generator, with the modulus equal to a power of two, and an odd value for has been shown to be an integer multiple of (see Wikramaratna (1992)). Therefore, increasing will give a series with a longer period.
 L'Ecuyer MRG32k3a Combined Recursive Generator
L'Ecuyer MRG32k3a Combined Recursive Generator
The base generator L'Ecuyer MRG32k3a (see L'Ecuyer and Simard (2002)) combines two multiple recursive generators:
where , , , , , , , , and form the required sequence. If then else if then . Combining the two multiple recursive generators (MRG) results in sequences with better statistical properties in high dimensions and longer periods compared with those generated from a single MRG. The combined generator described above has a period length of approximately .
 Quasi-random Numbers
Quasi-random Numbers
Low discrepancy (quasi-random) sequences are used in numerical integration, simulation and optimization. Like pseudorandom numbers they are uniformly distributed but they are not statistically independent, rather they are designed to give more even distribution in multidimensional space (uniformity). Therefore they are often more efficient than pseudorandom numbers in multidimensional Monte–Carlo methods.
The quasi-random number generators implemented in this chapter generate a set of points with high uniformity in the -dimensional unit cube . One measure of the uniformity is the discrepancy which is defined as follows:
- Given a set of points and a subset , define the counting function as the number of points . For each , let be the rectangular -dimensional region
with volume . Then the discrepancy of the points isThe discrepancy of the first terms of such a sequence has the formThe principal aim in the construction of low-discrepancy sequences is to find sequences of points in with a bound of this form where the constant is as small as possible.
Three types of low-discrepancy sequences are supplied in this library, these are due to Sobol, Faure and Niederreiter. Two sets of Sobol sequences are supplied, the first is based on work of Joe and Kuo (2008) and the second on the work of Bratley and Fox (1988). More information on quasi-random number generation and the Sobol, Faure and Niederreiter sequences in particular can be found in Bratley and Fox (1988) and Fox (1986).
The efficiency of a simulation exercise may often be increased by the use of variance reduction methods (see Morgan (1984)). It is also worth considering whether a simulation is the best approach to solving the problem. For example, low-dimensional integrals are usually more efficiently calculated by methods in D01 class rather than by Monte–Carlo integration.
 Scrambled Quasi-random Numbers
Scrambled Quasi-random Numbers
Scrambled quasi-random sequences are an extension of standard quasi-random sequences that attempt to eliminate the bias inherent in a quasi-random sequence whilst retaining the low-discrepancy properties. The use of a scrambled sequence allows error estimation of Monte–Carlo results by performing a number of iterates and computing the variance of the results.
This implementation of scrambled quasi-random sequences is based on TOMS algorithm 823 and details can be found in the accompanying paper, Hong and Hickernell (2003). Three methods of scrambling are supplied; the first a restricted form of Owen's scrambling (Owen (1995)), the second based on the method of Faure and Tezuka (2000) and the last method combines the first two.
Scrambled versions of both Sobol sequences and the Niederreiter sequence can be obtained.
 Non-uniform Random Numbers
Non-uniform Random Numbers
Random numbers from other distributions may be obtained from the uniform random numbers by the use of transformations and rejection techniques, and for discrete distributions, by table based methods.
| (a) | Transformation Methods
For a continuous random variable, if the cumulative distribution function (CDF) is then for a uniform random variate , will have CDF . This method is only efficient in a few simple cases such as the exponential distribution with mean , in which case . Other transformations are based on the joint distribution of several random variables. In the bivariate case, if and are random variates there may be a function such that has the required distribution; for example, the Student's -distribution with degrees of freedom in which has a Normal distribution, has a gamma distribution and . |
| (b) | Rejection Methods
Rejection techniques are based on the ability to easily generate random numbers from a distribution (called the envelope) similar to the distribution required. The value from the envelope distribution is then accepted as a random number from the required distribution with a certain probability; otherwise, it is rejected and a new number is generated from the envelope distribution. |
| (c) | Table Search Methods
For discrete distributions, if the cumulative probabilities, , are stored in a table then, given from a uniform distribution, the table is searched for such that . The returned value will have the required distribution. The table searching can be made faster by means of an index, see Ripley (1987). The effort required to set up the table and its index may be considerable, but the methods are very efficient when many values are needed from the same distribution. |
 Copulas
Copulas
A copula is a function that links the univariate marginal distributions with their multivariate distribution. Sklar's theorem (see Sklar (1973)) states that if is an -dimensional distribution function with continuous margins , then has a unique copula representation, , such that
The copula, , is a multivariate uniform distribution whose dependence structure is defined by the dependence structure of the multivariate distribution , with
where . This relationship can be used to simulate variates from distributions defined by the dependence structure of one distribution and each of the marginal distributions given by another. For additional information see Nelsen (1998) or Boye (Unpublished manuscript) and the references therein.
 Brownian Bridge
Brownian Bridge
 Brownian Bridge Process
Brownian Bridge Process
Fix two times and let be a standard -dimensional Wiener process on the interval . Recall that the terms Wiener process and Brownian motion are often used interchangeably.
The process is continuous, starts at zero at time and ends at zero at time . It is Gaussian, has zero mean and has a covariance structure given by
for any in where is the -dimensional identity matrix. The Brownian bridge is often called a non-free or ‘pinned’ Wiener process since it is forced to be at time , but is otherwise very similar to a standard Wiener process.
We can generalize this construction as follows. Fix points , let be a covariance matrix and choose any matrix such that . The generalized -dimensional Brownian bridge is defined by setting
for all . The process is continuous, starts at at time and ends at at time . It has mean and covariance structure
for all in . This is a non-free Wiener process since it is forced to be equal to at time . However if we set , then simplifies to
for all which is nothing other than a -dimensional Wiener process with covariance given by .
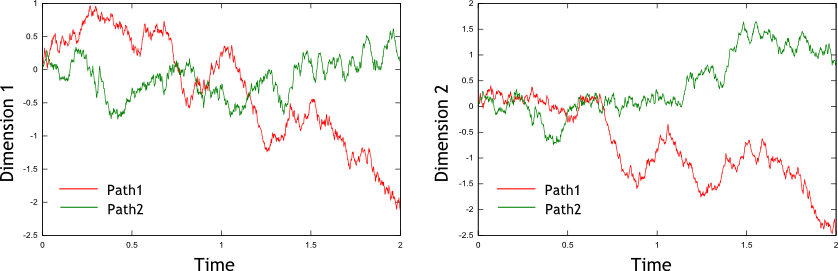
Figure 1: Two sample paths for a two-dimensional free Wiener process
Figure 2: Two sample paths for a two-dimensional free Wiener process
Figure 1 shows two sample paths for a two-dimensional free Wiener process . The correlation coefficient between the one-dimensional processes and at any time is . Note that the red and green paths in each figure are uncorrelated, however it is fairly evident that the two red paths are correlated, and that the two green paths are correlated (when one path increases so does the other, and vice versa).
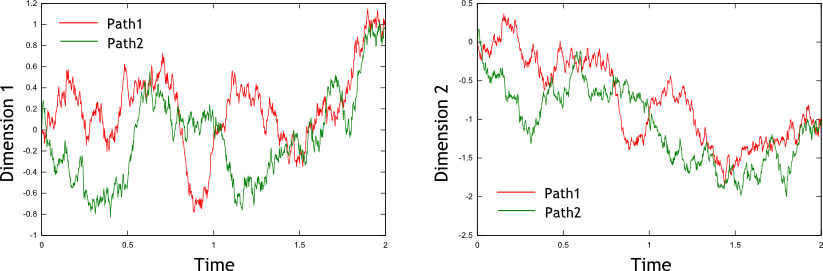
Figure 3: Two sample paths for a two-dimensional non-free Wiener process. The process starts at and ends at
Figure 4: Two sample paths for a two-dimensional non-free Wiener process. The process starts at and ends at
Figure 2 shows two sample paths for a two-dimensional non-free Wiener process. The process starts at and ends at . The correlation coefficient between the one-dimensional processes is again . The red and green paths in each figure are uncorrelated, while the two red paths tend to increase and decrease together, as do the two green paths. Both Figure 1 and Figure 2 were constructed using (G05XBF not in this release).
 Brownian Bridge Algorithm
Brownian Bridge Algorithm
The ideas above can also be used to construct sample paths of a free or non-free Wiener process (recall that a non-free Wiener process is the Brownian bridge process outlined above). Fix two times and let be any set of time points satisfying . Let denote a -dimensional (free or non-free) Wiener sample path at these times. These values can be generated by the so-called Brownian bridge algorithm (see Glasserman (2004)) which works as follows. From any two known points at time and at time with , a new point can be interpolated at any time by setting
where is a -dimensional standard Normal random variable and is any matrix such that is the desired covariance structure for the (free or non-free) Wiener process . Clearly this algorithm is iterative in nature. All that is needed to complete the specification is to fix the start point and end point , and to specify how successive interpolation times are chosen. For to behave like a usual (free) Wiener process we should set equal to some value and then set where is any -dimensional standard Normal random variable. However when it comes to deciding how the successive interpolation times should be chosen, there is virtually no restriction. Any method of choosing which to interpolate next is equally valid, provided is the nearest known point to the left of and is the nearest known point to the right of . In other words, the interpolation interval must not contain any other known points, otherwise the covariance structure of the process will be incorrect.
| (2) |
The order in which the successive interpolation times are chosen is called the bridge construction order. Since all construction orders will produce a correct process, the question arises whether one construction order should be preferred over another. When the values are drawn from a pseudorandom generator, the answer is typically no. However the bridge algorithm is frequently used with quasi-random numbers, and in this case the bridge construction order can be important.
 Bridge Construction Order and Quasi-random Sequences
Bridge Construction Order and Quasi-random Sequences
Consider the one-dimensional case of a free Wiener process where . The Brownian bridge is frequently combined with low-discrepancy (quasi-random) sequences to perform quasi-Monte–Carlo integration. Quasi-random points are generated from the standard Normal distribution, where each quasi-random point consists of one-dimensional values. The process starts at which is known. There remain time points at which the bridge is to be computed, namely and (recall we are considering a free Wiener process). In this case is set equal to , so that dimensional quasi-random points are generated. A single quasi-random point is used to construct one Wiener sample path.
The question is how to use the dimension values of each dimensional quasi-random point. Often the ‘lower’ dimension values (, etc.) display better uniformity properties than the ‘higher’ dimension values (, etc.) so that the ‘lower’ dimension values should be used to construct the most important sections of the sample path. For example, consider a model which is particularly sensitive to the behaviour of the underlying process at time . When constructing the sample paths, one would therefore ensure that time was one of the interpolation points of the bridge, and that a ‘lower’ dimension value was used in (2) to construct the corresponding bridge point . Indeed, one would most likely also ensure that time was one of the first bridge points that was constructed: ‘lower’ dimension values would be used to construct both the left and right bridge points used in (2) to interpolate , so that the distribution of benefits as much as possible from the uniformity properties of the quasi-random sequence. For further discussions in this regard we refer to Glasserman (2004). These remarks extend readily to the case of a non-free Wiener process.
 Brownian Bridge and Stochastic Differential Equations
Brownian Bridge and Stochastic Differential Equations
The Brownian bridge algorithm, especially when combined with quasi-random variates, is frequently used to obtain numerical solutions to stochastic differential equations (SDEs) driven by (free or non-free) Wiener processes. The quasi-random variates produce a family of Wiener sample paths which cover the space of all Wiener sample paths fairly evenly. This is analogous to the way in which a two-dimensional quasi-random sequence covers the unit square evenly. When solving SDEs one is typically interested in the increments of the driving Wiener process between two time points, rather than the value of the process at a particular time point. [Brownian Bridge] contains details on which methods can be used to obtain such Wiener increments.
 Random Fields
Random Fields
A random field is a stochastic process, taking values in a Euclidean space, and defined over a parameter space of dimensionality at least one. They are often used to simulate some physical space-dependent parameter, such as the permeability of rock, which cannot be measured at every point in the space. The simulated values can then be used to model other dependent quantities, for example, underground flow of water, often through the use of partial differential equations (PDEs).
A -dimensional random field is a function which is random at every point for some domain , so is a random variable for each . The random field has a mean function and a symmetric positive semidefinite covariance function .
A random field, , is a Gaussian random field if, for any choice of and , the random vector follows a multivariate Gaussian distribution.
A Gaussian random field is stationary if is constant for all and for all and hence we can express the covariance function as a function of one variable: . is known as a variogram (or more correctly, a semivariogram) and includes the multiplicative factor representing the variance such that . There are a number of commonly used variograms, including:
where is a scaled norm of .
| 1.Symmetric stable variogram |
|
||
| 2.Cauchy variogram |
|
||
| 3.Differential variogram with compact support |
|
||
| 4.Exponential variogram |
|
||
| 5.Gaussian variogram |
|
||
| 6.Nugget variogram |
|
||
| 7.Spherical variogram |
|
||
| 8.Bessel variogram |
|
||
| 9.Hole effect variogram |
|
||
| 10.Whittle–Matérn variogram |
|
||
| 11.Continuously parameterised variogram with compact support |
|
||
| 12.Generalized hyperbolic distribution variogram |
|
||
| 13.Cosine variogram |
|
 Other Random Structures
Other Random Structures
In addition to random numbers from various distributions, random compound structures can be generated. These include random time series, random matrices and random samples.
 Multiple Streams of Pseudorandom Numbers
Multiple Streams of Pseudorandom Numbers
It is often advantageous to be able to generate variates from multiple, independent, streams (or sequences) of random variates. For example when running a simulation in parallel on several processors. There are four ways of generating multiple streams using the methods available in this chapter:
| (i) | using different initial values (seeds); |
| (ii) | using different generators; |
| (iii) | skip ahead (also called block-splitting); |
| (iv) | leap-frogging. |
 Multiple Streams via Different Initial Values (Seeds)
Multiple Streams via Different Initial Values (Seeds)
A different sequence of variates can be generated from the same base generator by initializing the generator using a different set of seeds. The statistical properties of the base generators are only guaranteed within, not between sequences. For example, two sequences generated from two different starting points may overlap if these initial values are not far enough apart. The potential for overlapping sequences is reduced if the period of the generator being used is large. In general, of the four methods for creating multiple streams described here, this is the least satisfactory.
The one exception to this is the Wichmann–Hill II generator. The Wichmann and Hill (2006) paper describes a method of generating blocks of variates, with lengths up to , by fixing the first three seed values of the generator (, and ), and setting to a different value for each stream required. This is similar to the skip-ahead method described in [Multiple Streams via Skip-ahead], in that the full sequence of the Wichmann–Hill II generator is split into a number of different blocks, in this case with a fixed length of . But without the computationally intensive initialization usually required for the skip-ahead method.
 Multiple Streams via Different Generators
Multiple Streams via Different Generators
Independent sequences of variates can be generated using a different base generator for each sequence. For example, sequence 1 can be generated using the NAG basic generator, sequence 2 using Mersenne Twister, sequence 3 the ACORN generator and sequence 4 using L'Ecuyer generator. The Wichmann–Hill I generator implemented in this chapter is, in fact, a series of 273 independent generators. The particular sub-generator to use is selected using the subid variable. Therefore, in total, 278 independent streams can be generated with each using a different generator (273 Wichmann–Hill I generators, and 5 additional base generators).
 Multiple Streams via Skip-ahead
Multiple Streams via Skip-ahead
Independent sequences of variates can be generated from a single base generator through the use of block-splitting, or skipping-ahead. This method consists of splitting the sequence into non-overlapping blocks, each of length , where is no smaller than the maximum number of variates required from any of the sequences. For example,
where is the sequence produced by the generator of interest. Each of the blocks provide an independent sequence.
The skip-ahead algorithm therefore requires the sequence to be advanced a large number of places, as to generate values from say, block , you must skip over the values in the first blocks. Due to their form this can be done efficiently for linear congruential generators and multiple congruential generators. A skip-ahead algorithm is also provided for the Mersenne Twister generator.
Although skip-ahead requires some additional computation at the initialization stage (to ‘fast forward’ the sequence) no additional computation is required at the generation stage.
 Multiple Streams via Leap-frog
Multiple Streams via Leap-frog
Independent sequences of variates can also be generated from a single base generator through the use of leap-frogging. This method involves splitting the sequence from a single generator into disjoint subsequences. For example:
where is the sequence produced by the generator of interest. Each of the subsequences then provides an independent stream of variates.
The leap-frog algorithm therefore requires the generation of every th variate from the base generator. Due to their form this can be done efficiently for linear congruential generators and multiple congruential generators. A leap-frog algorithm is provided for the NAG Basic generator, both the Wichmann–Hill I and Wichmann–Hill II generators and L'Ecuyer generator.
It is known that, dependent on the number of streams required, leap-frogging can lead to sequences with poor statistical properties, especially when applied to linear congruential generators. In addition, leap-frogging can increase the time required to generate each variate. Therefore leap-frogging should be avoided unless absolutely necessary.
 Skip-ahead and Leap-frog for a Linear Congruential Generator (LCG): An Example
Skip-ahead and Leap-frog for a Linear Congruential Generator (LCG): An Example
As an illustrative example, a brief description of the algebra behind the implementation of the leap-frog and skip-ahead algorithms for a linear congruential generator is given. A linear congruential generator has the form . The recursive nature of a linear congruential generator means that
The sequence can therefore be quickly advanced places by multiplying the current state () by , hence skipping the sequence ahead. Leap-frogging can be implemented by using , where is the number of streams required, in place of in the standard linear congruential generator recursive formula, in order to advance places, rather than one, at each iteration.
In a linear congruential generator the multiplier is constructed so that the generator has good statistical properties in, for example, the spectral test. When using leap-frogging to construct multiple streams this multiplier is replaced with , and there is no guarantee that this new multiplier will have suitable properties especially as the value of depends on the number of streams required and so is likely to change depending on the application. This problem can be emphasized by the lattice structure of linear congruential generators. Similiarly, the value of is often chosen such that the computation can be performed efficiently. When is replaced by , this is often no longer the case.
Note that, due to rounding, when using a distributional generator, a sequence generated using leap-frogging and a sequence constructed by taking every value from a set of variates generated without leap-frogging may differ slightly. These differences should only affect the least significant digit.
 Skip-ahead and Leap-frog for the Mersenne Twister: An Example
Skip-ahead and Leap-frog for the Mersenne Twister: An Example
Skipping ahead with the Mersenne Twister generator is based on the definition of a (where ) transition matrix, , over the finite field (with elements 0 and 1). Multiplying by the current state , represented as a vector of bits, produces the next state vector :
Thus, skipping ahead places in a sequence is equivalent to multiplying by :
Since calculating by a standard square and multiply algorithm is and requires over 47MB of memory (see Haramoto et al. (2008)), an indirect calculation is performed which relies on a property of the characteristic polynomial of , namely that . We then define
and observe that
for a polynomial . Since , we have that and
This polynomial evaluation can be performed using Horner's method:
which reduces the problem to advancing the generator places from state and adding (where addition is as defined over ) the intermediate states for which is nonzero.
There are therefore two stages to skipping the Mersenne Twister ahead places:
| (i) | Calculate the coefficients of the polynomial ; |
| (ii) | advance the sequence places from the starting state and add the intermediate states that correspond to nonzero coefficients in the polynomial calculated in the first step. |
The resulting state is that for position in the sequence.
The cost of calculating the polynomial is and the cost of applying it to state is constant. Skip ahead functionality is typically used in order to generate independent pseudorandom number streams (e.g., for separate threads of computation). There are two options for generating the states:
| (i) | On the master thread calculate the polynomial for a skip ahead distance of and apply this polynomial to state times, after each iteration saving the current state for later usage by thread . |
| (ii) | Have each thread independently and in parallel with other threads calculate the polynomial for a distance of and apply to the original state. |
Since
, then for large the cost of generating the polynomial for a skip ahead distance of (i.e., the calculation performed by thread in option (ii) above) is approximately the same as generating that for a distance of (i.e., the calculation performed by thread ). However, only one application to state need be made per thread, and if is sufficiently large the cost of applying the polynomial to state becomes the dominant cost in option (i), in which case it is desirable to use option (ii). Tests have shown that as a guideline it becomes worthwhile to switch from option (i) to option (ii) for approximately .
Leap frog calculations with the Mersenne Twister are performed by computing the sequence fully up to the required size and discarding the redundant numbers for a given stream.
 Recommendations on Choice and Use of Available Methods
Recommendations on Choice and Use of Available Methods
 Pseudorandom Numbers
Pseudorandom Numbers
Prior to generating any pseudorandom variates the base generator being used must be initialized. Once initialized, a distributional generator can be called to obtain the variates required. No interfaces have been supplied for direct access to the base generators. If a sequence of random variates from a uniform distribution on the open interval , is required, then the uniform distribution method (g05sa) should be called.
 Initialization
Initialization
Prior to generating any variates the base generator must be initialized. Two utility methods are provided for this, (G05KFF not in this release) and (G05KGF not in this release), both of which allow any of the base generators to be chosen.
(G05KFF not in this release) selects and initializes a base generator to a repeatable (when executed serially) state: two calls of (G05KFF not in this release) with the same argument-values will result in the same subsequent sequences of random numbers (when both generated serially).
(G05KGF not in this release) selects and initializes a base generator to a non-repeatable state in such a way that different calls of (G05KGF not in this release), either in the same run or different runs of the program, will almost certainly result in different subsequent sequences of random numbers.
No utilities for saving, retrieving or copying the current state of a generator have been provided. All of the information on the current state of a generator (or stream, if multiple streams are being used) is stored in the integer array state and as such this array can be treated as any other integer array, allowing for easy copying, restoring, etc.
 Repeated initialization
Repeated initialization
As mentioned in [Multiple Streams via Different Initial Values (Seeds)], it is important to note that the statistical properties of pseudorandom numbers are only guaranteed within sequences and not between sequences produced by the same generator. Repeated initialization will thus render the numbers obtained less rather than more independent. In a simple case there should be only one call to (G05KFF not in this release) (G05KGF not in this release) and this call should be before any call to an actual generation method.
 Choice of Base Generator
Choice of Base Generator
If a single sequence is required then it is recommended that the Mersenne Twister is used as the base generator (). This generator is fast, has an extremely long period and has been shown to perform well on various test suites, see Matsumoto and Nishimura (1998), L'Ecuyer and Simard (2002) and Wichmann and Hill (2006) for example.
When choosing a base generator, the period of the chosen generator should be borne in mind. A good rule of thumb is never to use more numbers than the square root of the period in any one experiment as the statistical properties are impaired. For closely related reasons, breaking numbers down into their bit patterns and using individual bits may also cause trouble.
 Choice of Method for Generating Multiple Streams
Choice of Method for Generating Multiple Streams
If the Wichmann–Hill II base generator is being used, and a period of is sufficient, then the method described in [Multiple Streams via Different Initial Values (Seeds)] can be used. If a different generator is used, or a longer period length is required then generating multiple streams by altering the initial values should be avoided.
Using a different generator works well if less than 277 streams are required.
Of the remaining two methods, both skip-ahead and leap-frogging use the sequence from a single generator, both guarantee that the different sequences will not overlap and both can be scaled to an arbitrary number of streams. Leap-frogging requires no a-priori knowledge about the number of variates being generated, whereas skip-ahead requires you to know (approximately) the maximum number of variates required from each stream. Skip-ahead requires no a-priori information on the number of streams required. In contrast leap-frogging requires you to know the maximum number of streams required, prior to generating the first value. Of these two, if possible, skip-ahead should be used in preference to leap-frogging. Both methods required additional computation compared with generating a single sequence, but for skip-ahead this computation occurs only at initialization. For leap-frogging additional computation is required both at initialization and during the generation of the variates. In addition, as mentioned in [Multiple Streams via Leap-frog], using leap-frogging can, in some instances, change the statistical properties of the sequences being generated.
Leap-frogging is performed by calling g05kh after the initialization method ( (G05KFF not in this release) (G05KGF not in this release)). For skip-ahead, either g05kj or g05kk can be called. Of these, g05kk restricts the amount being skipped to a power of , but allows for a large ‘skip’ to be performed.
 Copulas
Copulas
After calling one of the copula methods the inverse cumulative distribution function (CDF) can be applied to convert the uniform marginal distribution into the required form. Scalar and vector routines for evaluating the CDF, for a range of distributions, are supplied in G01 class. It should be noted that these routines are often described as computing the ‘deviates’ of the distribution.
When using the inverse CDF methods from G01 class it should be noted that some are limited in the number of significant figures they return. This may affect the statistical properties of the resulting sequence of variates. Section 7 of the individual method documentation will give a discussion of the accuracy of the particular algorithm being used and any available alternatives.
 Quasi-random Numbers
Quasi-random Numbers
Prior to generating any quasi-random variates the generator being used must be initialized via g05yl or g05yn. Of these, g05yl can be used to initialize a standard Sobol, Faure or Niederreiter sequence and g05yn can be used to initialize a scrambled Sobol or Niederreiter sequence.
Due to the random nature of the scrambling, prior to calling the initialization method g05yn one of the pseudorandom initialization methods, (G05KFF not in this release) (G05KGF not in this release), must be called.
Once a quasi-random generator has been initialized, using either g05yl or g05yn, one of three generation methods can be called to generate uniformly distributed sequences (g05ym), Normally distributed sequences ( (G05YJF not in this release)) or sequences with a log-normal distribution ( (G05YKF not in this release)). For example, for a repeatable sequence of scrambled quasi-random variates from the Normal distribution, (G05KFF not in this release) must be called first (to initialize a pseudorandom generator), followed by g05yn (to initialize a scrambled quasi-random generator) and then (G05YJF not in this release) can be called to generate the sequence from the required distribution.
See the last paragraph of [Copulas] on how sequences from other distributions can be obtained using the inverse CDF.
 Brownian Bridge
Brownian Bridge
(G05XBF not in this release) may be used to generate sample paths from a (free or non-free) Wiener process using the Brownian bridge algorithm. Prior to calling (G05XBF not in this release), the generator must be initialized by a call to (G05XAF not in this release). (G05XAF not in this release) requires you to specify a bridge construction order. The method (G05XEF not in this release) can be used to convert a set of input times into one of several common bridge construction orders, which can then be used in the initialization call to (G05XAF not in this release).
(G05XDF not in this release) may be used to generate the scaled increments of the sample paths of a (free or non-free) Wiener process. Prior to calling (G05XDF not in this release), the generator must be initialized by a call to (G05XCF not in this release). Note that (G05XDF not in this release) generates these scaled increments directly; it is not necessary to call (G05XBF not in this release) before calling (G05XDF not in this release). As before, (G05XEF not in this release) can be used to convert a set of input times into a bridge construction order which can be passed to (G05XCF not in this release).
 Random Fields
Random Fields
Methods for simulating from either a one-dimensional or a two-dimensional stationary Gaussian random field are provided. These methods use the circulant embedding method of Dietrich and Newsam (1997) to efficiently generate from the required field. In both cases a setup method is called, which defines the domain and variogram to use, followed by the generation method. A number of preset variograms are supplied or a user-defined method can be used.
- One-dimensional random field:
- (G05ZNF not in this release) setup method, using a preset variogram.
- (G05ZMF not in this release) setup method, using a user-defined variogram.
- (G05ZPF not in this release) generation method.
- Two-dimension random field:
- (G05ZQF not in this release) setup method, using a preset variogram.
- (G05ZRF not in this release) setup method, using a user-defined variogram.
- (G05ZSF not in this release) generation method.
In addition to generating a random field, it is possible to use the circulant embedding method to generate realizations of fractional Brownian motion, this functionality is provided in (G05ZTF not in this release).
Prior to calling (G05ZPF not in this release), (G05ZRF not in this release) or (G05ZTF not in this release) one of the initialization methods, (G05KFF not in this release) or (G05KGF not in this release) must be called.
 References
References
Banks J (1998) Handbook on Simulation Wiley
Boye E (Unpublished manuscript) Copulas for finance: a reading guide and some applications Financial Econometrics Research Centre, City University Business School, London
Bratley P and Fox B L (1988) Algorithm 659: implementing Sobol's quasirandom sequence generator ACM Trans. Math. Software 14(1) 88–100
Dietrich C R and Newsam G N (1997) Fast and exact simulation of stationary Gaussian processes through circulant embedding of the covariance matrix SIAM J. Sci. Comput. 18 1088–1107
Faure H and Tezuka S (2000) Another random scrambling of digital (t,s)-sequences Monte Carlo and Quasi-Monte Carlo Methods Springer-Verlag, Berlin, Germany (eds K T Fang, F J Hickernell and H Niederreiter)
Fox B L (1986) Algorithm 647: implementation and relative efficiency of quasirandom sequence generators ACM Trans. Math. Software 12(4) 362–376
Glasserman P (2004) Monte Carlo Methods in Financial Engineering Springer
Haramoto H, Matsumoto M, Nishimura T, Panneton F and L'Ecuyer P (2008) Efficient jump ahead for F2-linear random number generators INFORMS J. on Computing 20(3) 385–390
Hong H S and Hickernell F J (2003) Algorithm 823: implementing scrambled digital sequences ACM Trans. Math. Software 29:2 95–109
Joe S and Kuo F Y (2008) Constructing Sobol sequences with better two-dimensional projections SIAM J. Sci. Comput. 30 2635–2654
Knuth D E (1981) The Art of Computer Programming (Volume 2) (2nd Edition) Addison–Wesley
L'Ecuyer P and Simard R (2002) TestU01: a software library in ANSI C for empirical testing of random number generators Departement d'Informatique et de Recherche Operationnelle, Universite de Montreal http://www.iro.umontreal.ca/~lecuyer
Maclaren N M (1989) The generation of multiple independent sequences of pseudorandom numbers Appl. Statist. 38 351–359
Matsumoto M and Nishimura T (1998) Mersenne twister: a 623-dimensionally equidistributed uniform pseudorandom number generator ACM Transactions on Modelling and Computer Simulations
Morgan B J T (1984) Elements of Simulation Chapman and Hall
Nelsen R B (1998) An Introduction to Copulas. Lecture Notes in Statistics 139 Springer
Owen A B (1995) Randomly permuted (t,m,s)-nets and (t,s)-sequences Monte Carlo and Quasi-Monte Carlo Methods in Scientific Computing, Lecture Notes in Statistics 106 Springer-Verlag, New York, NY 299–317 (eds H Niederreiter and P J-S Shiue)
Revuz D and Yor M (1999) Continuous Martingales and Brownian Motion Springer
Ripley B D (1987) Stochastic Simulation Wiley
Sklar A (1973) Random variables: joint distribution functions and copulas Kybernetika 9 499–460
Wichmann B A and Hill I D (2006) Generating good pseudo-random numbers Computational Statistics and Data Analysis 51 1614–1622
Wikramaratna R S (1989) ACORN - a new method for generating sequences of uniformly distributed pseudo-random numbers Journal of Computational Physics 83 16–31
Wikramaratna R S (1992) Theoretical background for the ACORN random number generator Report AEA-APS-0244 AEA Technology, Winfrith, Dorest, UK
Wikramaratna R S (2007) The additive congruential random number generator a special case of a multiple recursive generator Journal of Computational and Applied Mathematics