s13aa returns the value of the exponential integral .
 Syntax
Syntax
| C# |
|---|
public static double s13aa( double x, out int ifail ) |
| Visual Basic |
|---|
Public Shared Function s13aa ( _ x As Double, _ <OutAttribute> ByRef ifail As Integer _ ) As Double |
| Visual C++ |
|---|
public: static double s13aa( double x, [OutAttribute] int% ifail ) |
| F# |
|---|
static member s13aa : x : float * ifail : int byref -> float |
Parameters
- x
- Type: System..::..DoubleOn entry: the argument of the function.Constraint: or .
- ifail
- Type: System..::..Int32%On exit: unless the method detects an error or a warning has been flagged (see [Error Indicators and Warnings]).
Return Value
s13aa returns the value of the exponential integral .
 Description
Description
s13aa calculates an approximate value for
using Chebyshev expansions, where is real. For , the real part of the principal value of the integral is taken. The value is infinite, and so, when , s13aa exits with an error and returns the largest representable machine number.
For ,
where .
For ,
where .
In both cases, .
For , the approximation is based on expansions proposed by Cody and Thatcher Jr. (1969). Precautions are taken to maintain good relative accuracy in the vicinity of , which corresponds to a simple zero of Ei().
s13aa guards against producing underflows and overflows by using the parameter ; see the Users' Note for your implementation for the value of . To guard against overflow, if the method terminates and returns the negative of the largest representable machine number. To guard against underflow, if the result is set directly to zero.
 References
References
Abramowitz M and Stegun I A (1972) Handbook of Mathematical Functions (3rd Edition) Dover Publications
Cody W J and Thatcher Jr. H C (1969) Rational Chebyshev approximations for the exponential integral Ei Math. Comp. 23 289–303
 Error Indicators and Warnings
Error Indicators and Warnings
Errors or warnings detected by the method:
- On entry, and the function is infinite. The result returned is the largest representable machine number.
- The evaluation has been abandoned due to the likelihood of overflow. The argument , and the result is returned as the negative of the largest representable machine number.
 Accuracy
Accuracy
Unless stated otherwise, it is assumed that .
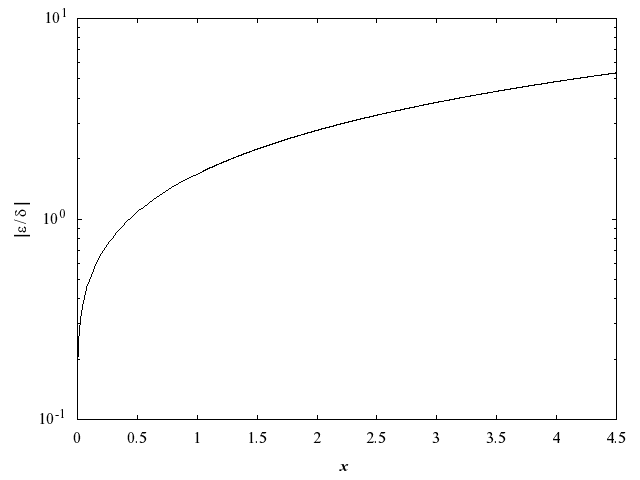
If and are the relative errors in argument and result respectively, then in principle,
so the relative error in the argument is amplified in the result by at least a factor . The equality should hold if is greater than the machine precision ( due to data errors etc.) but if is simply a result of round-off in the machine representation, it is possible that an extra figure may be lost in internal calculation and round-off.
It should be noted that, for absolutely small , the amplification factor tends to zero and eventually the error in the result will be limited by machine precision.
For absolutely large ,
the absolute error in the argument.
For , empirical tests have shown that the maximum relative error is a loss of approximately decimal place.
 Parallelism and Performance
Parallelism and Performance
None.
 Further Comments
Further Comments
None.
 Example
Example
The following program reads values of the argument from a file, evaluates the function at each value of and prints the results.
Example program (C#): s13aae.cs