This chapter is concerned with two techniques – correlation analysis and regression modelling – both of which are concerned with determining the inter-relationships among two or more variables.
Other chapters of the NAG Library which cover similar problems are E02 class E04 class. E02 class methods may be used to fit linear models by criteria other than least squares, and also for polynomial regression; E04 class methods may be used to fit nonlinear models and linearly constrained linear models.
 Syntax
Syntax
| C# |
|---|
public static class G02 |
| Visual Basic |
|---|
Public NotInheritable Class G02 |
| Visual C++ |
|---|
public ref class G02 abstract sealed |
| F# |
|---|
[<AbstractClassAttribute>] [<SealedAttribute>] type G02 = class end |
 Background to the Problems
Background to the Problems
 Correlation
Correlation
 Aims of correlation analysis
Aims of correlation analysis
Correlation analysis provides a single summary statistic – the correlation coefficient – describing the strength of the association between two variables. The most common types of association which are investigated by correlation analysis are linear relationships, and there are a number of forms of linear correlation coefficients for use with different types of data.
 Correlation coefficients
Correlation coefficients
The (Pearson) product-moment correlation coefficients measure a linear relationship, while Kendall's tau and Spearman's rank order correlation coefficients measure monotonicity only. All three coefficients range from to . A coefficient of zero always indicates that no linear relationship exists; a coefficient implies a ‘perfect’ positive relationship (i.e., an increase in one variable is always associated with a corresponding increase in the other variable); and a coefficient of indicates a ‘perfect’ negative relationship (i.e., an increase in one variable is always associated with a corresponding decrease in the other variable).
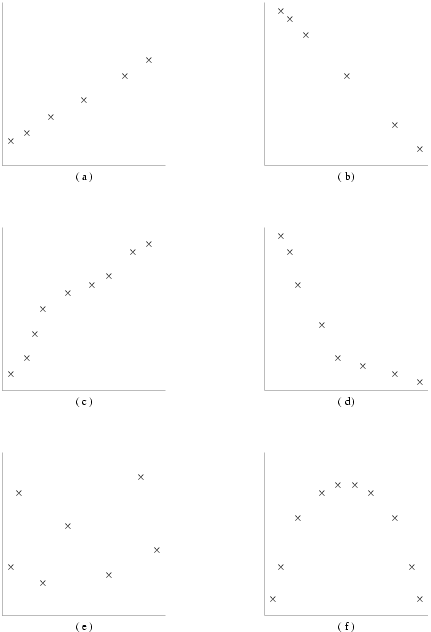
Consider the bivariate scattergrams in Figure 1: (a) and (b) show strictly linear functions for which the values of the product-moment correlation coefficient, and (since a linear function is also monotonic) both Kendall's tau and Spearman's rank order coefficients, would be and respectively. However, though the relationships in figures (c) and (d) are respectively monotonically increasing and monotonically decreasing, for which both Kendall's and Spearman's nonparametric coefficients would be (in (c)) and (in (d)), the functions are nonlinear so that the product-moment coefficients would not take such ‘perfect’ extreme values. There is no obvious relationship between the variables in figure (e), so all three coefficients would assume values close to zero, while in figure (f) though there is an obvious parabolic relationship between the two variables, it would not be detected by any of the correlation coefficients which would again take values near to zero; it is important therefore to examine scattergrams as well as the correlation coefficients.
In order to decide which type of correlation is the most appropriate, it is necessary to appreciate the different groups into which variables may be classified. Variables are generally divided into four types of scales: the nominal scale, the ordinal scale, the interval scale, and the ratio scale. The nominal scale is used only to categorise data; for each category a name, perhaps numeric, is assigned so that two different categories will be identified by distinct names. The ordinal scale, as well as categorising the observations, orders the categories. Each category is assigned a distinct identifying symbol, in such a way that the order of the symbols corresponds to the order of the categories. (The most common system for ordinal variables is to assign numerical identifiers to the categories, though if they have previously been assigned alphabetic characters, these may be transformed to a numerical system by any convenient method which preserves the ordering of the categories.) The interval scale not only categorises and orders the observations, but also quantifies the comparison between categories; this necessitates a common unit of measurement and an arbitrary zero-point. Finally, the ratio scale is similar to the interval scale, except that it has an absolute (as opposed to arbitrary) zero-point.
For a more complete discussion of these four types of scales, and some examples, you are referred to Churchman and Ratoosh (1959) and Hays (1970).
Figure 1
Product-moment correlation coefficients are used with variables which are interval (or ratio) scales; these coefficients measure the amount of spread about the linear least squares equation. For a product-moment correlation coefficient, , based on pairs of observations, testing against the null hypothesis that there is no correlation between the two variables, the statistic
has a Student's -distribution with degrees of freedom; its significance can be tested accordingly.
Ranked and ordinal scale data are generally analysed by nonparametric methods – usually either Spearman's or Kendall's tau rank order correlation coefficients, which, as their names suggest, operate solely on the ranks, or relative orders, of the data values. Interval or ratio scale variables may also be validly analysed by nonparametric methods, but such techniques are statistically less powerful than a product-moment method. For a Spearman rank order correlation coefficient, , based on pairs of observations, testing against the null hypothesis that there is no correlation between the two variables, for large samples the statistic
has approximately a Student's -distribution with degrees of freedom, and may be treated accordingly. (This is similar to the product-moment correlation coefficient, , see above.) Kendall's tau coefficient, based on pairs of observations, has, for large samples, an approximately Normal distribution with mean zero and standard deviation
when tested against the null hypothesis that there is no correlation between the two variables; the coefficient should therefore be divided by this standard deviation and tested against the standard Normal distribution, .
When the number of ordinal categories a variable takes is large, and the number of ties is relatively small, Spearman's rank order correlation coefficients have advantages over Kendall's tau; conversely, when the number of categories is small, or there are a large number of ties, Kendall's tau is usually preferred. Thus when the ordinal scale is more or less continuous, Spearman's rank order coefficients are preferred, whereas Kendall's tau is used when the data is grouped into a smaller number of categories; both measures do however include corrections for the occurrence of ties, and the basic concepts underlying the two coefficients are quite similar. The absolute value of Kendall's tau coefficient tends to be slightly smaller than Spearman's coefficient for the same set of data.
There is no authoritative dictum on the selection of correlation coefficients – particularly on the advisability of using correlations with ordinal data. This is a matter of discretion for you.
 Partial correlation
Partial correlation
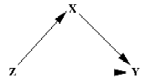
The correlation coefficients described above measure the association between two variables ignoring any other variables in the system. Suppose there are three variables and as shown in the path diagram below.
Figure 2
The association between and is made up of the direct association between and and the association caused by the path through , that is the association of both and with the third variable . For example if and were cholesterol level and blood pressure and were age since both blood pressure and cholesterol level may increase with age the correlation between blood pressure and cholesterol level eliminating the effect of age is required.The correlation between two variables eliminating the effect of a third variable is known as the partial correlation. If , and represent the correlations between , and then the partial correlation between and given is
The partial correlation is then estimated by using product-moment correlation coefficients.
In general, let a set of variables be partitioned into two groups and with variables in and variables in and let the variance-covariance matrix of all variables be partitioned into
Then the variance-covariance of conditional on fixed values of the variables is given by
The partial correlation matrix is then computed by standardizing .
 Robust estimation of correlation coefficients
Robust estimation of correlation coefficients
The product-moment correlation coefficient can be greatly affected by the presence of a few extreme observations or outliers. There are robust estimation procedures which aim to decrease the effect of extreme values.
Mathematically these methods can be described as follows. A robust estimate of the variance-covariance matrix, , can be written as
where is a correction factor to give an unbiased estimator if the data is Normal and is a lower triangular matrix. Let be the vector of values for the th observation and let , being a robust estimate of location, then and are found as solutions to
and
where , and are functions such that they return a value of for reasonable values of and decreasing values for large . The correlation matrix can then be calculated from the variance-covariance matrix. If , , and returned for all values then the product-moment correlation coefficient would be calculated.
 Missing values
Missing values
When there are missing values in the data these may be handled in one of two ways. Firstly, if a case contains a missing observation for any variable, then that case is omitted in its entirety from all calculations; this may be termed casewise treatment of missing data. Secondly, if a case contains a missing observation for any variable, then the case is omitted from only those calculations involving the variable for which the value is missing; this may be called pairwise treatment of missing data. Pairwise deletion of missing data has the advantage of using as much of the data as possible in the computation of each coefficient. In extreme circumstances, however, it can have the disadvantage of producing coefficients which are based on a different number of cases, and even on different selections of cases or samples; furthermore, the ‘correlation’ matrices formed in this way need not necessarily be positive semidefinite, a requirement for a correlation matrix. Casewise deletion of missing data generally causes fewer cases to be used in the calculation of the coefficients than does pairwise deletion. How great this difference is will obviously depend on the distribution of the missing data, both among cases and among variables.
Pairwise treatment does therefore use more information from the sample, but should not be used without careful consideration of the location of the missing observations in the data matrix, and the consequent effect of processing the missing data in that fashion.
 Nearest Correlation Matrix
Nearest Correlation Matrix
A correlation matrix is, by definition, a symmetric, positive semidefinite matrix with unit diagonals and all elements in the range .
In practice, rather than having a true correlation matrix, you may find that you have a matrix of pairwise correlations. This usually occurs in the presence of missing values, when the missing values are treated in a pairwise fashion as discussed in [Missing values]. Matrices constructed in this way may not be not positive semidefinite, and therefore are not a valid correlation matrix. However, a valid correlation matrix can be calculated that is in some sense ‘close’ to the original.
Given an matrix, , there are a number of available ways of computing the ‘nearest’ correlation matrix, to :
| (a) | Frobenius Norm
Find such that
Where is the symmetric matrix defined as and and denotes the elements of and respectively.
A weighted Frobenius norm can also be used. The term being summed across therefore becomes
if row and column weights are being used or
when element-wise weights are used.
|
||
| (b) | Factor Loading Method
This method is similar to (a) in that it finds a that is closest to in the Frobenius norm. However, it also ensures that has a -factor structure, that is can be written as
is often referred to as the factor loading matrix. This problem primarily arises when a factor model is used to describe a multivariate time series or collateralized debt obligations. In this model and are vectors of independent random variables having zero mean and unit variance, with and independent of each other, and with diagonal. In the case of modelling debt obligations can, for example, model the equity returns of different companies of a portfolio where describes factors influencing all companies, in contrast to the elements of having only an effect on the equity of the corresponding company. With this model the complex behaviour of a portfolio, with potentially thousands of equities, is captured by looking at the major factors driving the behaviour.
The number of factors usually chosen is a lot smaller than , perhaps between and , yielding a large reduction in the complexity. The number of the factors, , which yields a matrix such that is within a required tolerance can also be determined, by experimenting with the input and comparing the norms. |
 Regression
Regression
 Aims of regression modelling
Aims of regression modelling
In regression analysis the relationship between one specific random variable, the dependent or response variable, and one or more known variables, called the independent variables or covariates, is studied. This relationship is represented by a mathematical model, or an equation, which associates the dependent variable with the independent variables, together with a set of relevant assumptions. The independent variables are related to the dependent variable by a function, called the regression function, which involves a set of unknown parameters. Values of the parameters which give the best fit for a given set of data are obtained; these values are known as the estimates of the parameters.
The reasons for using a regression model are twofold. The first is to obtain a description of the relationship between the variables as an indicator of possible causality. The second reason is to predict the value of the dependent variable from a set of values of the independent variables. Accordingly, the most usual statistical problems involved in regression analysis are:
| (i) | to obtain best estimates of the unknown regression parameters; |
| (ii) | to test hypotheses about these parameters; |
| (iii) | to determine the adequacy of the assumed model; and |
| (iv) | to verify the set of relevant assumptions. |
 Regression models and designed experiments
Regression models and designed experiments
One application of regression models is in the analysis of experiments. In this case the model relates the dependent variable to qualitative independent variables known as factors. Factors may take a number of different values known as levels. For example, in an experiment in which one of four different treatments is applied, the model will have one factor with four levels. Each level of the factor can be represented by a dummy variable taking the values or . So in the example there are four dummy variables , for , such that:
along with a variable for the mean :
If there were observations the data would be:
When dummy variables are used it is common for the model not to be of full rank. In the case above, the model would not be of full rank because
This means that the effect of cannot be distinguished from the combined effect of and . This is known as aliasing. In this situation, the aliasing can be deduced from the experimental design and as a result the model to be fitted; in such situations it is known as intrinsic aliasing. In the example above no matter how many times each treatment is replicated (other than ) the aliasing will still be present. If the aliasing is due to a particular dataset to which the model is to be fitted then it is known as extrinsic aliasing. If in the example above observation was missing then the term would also be aliased. In general intrinsic aliasing may be overcome by changing the model, e.g., remove or from the model, or by introducing constraints on the parameters, e.g., .
If aliasing is present then there will no longer be a unique set of least squares estimates for the parameters of the model but the fitted values will still have a unique estimate. Some linear functions of the parameters will also have unique estimates; these are known as estimable functions. In the example given above the functions () and () are both estimable.
 Selecting the regression model
Selecting the regression model
In many situations there are several possible independent variables, not all of which may be needed in the model. In order to select a suitable set of independent variables, two basic approaches can be used.
| (a) | All possible regressions
In this case all the possible combinations of independent variables are fitted and the one considered the best selected. To choose the best, two conflicting criteria have to be balanced. One is the fit of the model which will improve as more variables are added to the model. The second criterion is the desire to have a model with a small number of significant terms. Depending on how the model is fit, statistics such as , which gives the proportion of variation explained by the model, and , which tries to balance the size of the residual sum of squares against the number of terms in the model, can be used to aid in the choice of model. |
| (b) | Stepwise model building
In stepwise model building the regression model is constructed recursively, adding or deleting the independent variables one at a time. When the model is built up the procedure is known as forward selection. The first step is to choose the single variable which is the best predictor. The second independent variable to be added to the regression equation is that which provides the best fit in conjunction with the first variable. Further variables are then added in this recursive fashion, adding at each step the optimum variable, given the other variables already in the equation. Alternatively, backward elimination can be used. This is when all variables are added and then the variables dropped one at a time, the variable dropped being the one which has the least effect on the fit of the model at that stage. There are also hybrid techniques which combine forward selection with backward elimination. |
 Linear Regression Models
Linear Regression Models
When the regression model is linear in the parameters (but not necessarily in the independent variables), then the regression model is said to be linear; otherwise the model is classified as nonlinear.
The most elementary form of regression model is the simple linear regression of the dependent variable, , on a single independent variable, , which takes the form
where is the expected or average value of and and are the parameters whose values are to be estimated, or, if the regression is required to pass through the origin (i.e., no constant term),
where is the only unknown parameter.
| (1) |
| (2) |
An extension of this is multiple linear regression in which the dependent variable, , is regressed on the () independent variables, , which takes the form
where and are the unknown parameters. Multiple linear regression models test include factors are sometimes known as General Linear (Regression) Models.
| (3) |
A special case of multiple linear regression is polynomial linear regression, in which the independent variables are in fact powers of the same single variable (i.e., , for ).
In this case, the model defined by (3) becomes
There are a great variety of nonlinear regression models; one of the most common is exponential regression, in which the equation may take the form
It should be noted that equation (4) represents a linear regression, since even though the equation is not linear in the independent variable, , it is linear in the parameters , whereas the regression model of equation (5) is nonlinear, as it is nonlinear in the parameters (, and ).
| (4) |
| (5) |
 Fitting the regression model – least squares estimation
Fitting the regression model – least squares estimation
One method used to determine values for the parameters is, based on a given set of data, to minimize the sums of squares of the differences between the observed values of the dependent variable and the values predicted by the regression equation for that set of data – hence the term least squares estimation. For example, if a regression model of the type given by equation (3), namely
where for all observations, is to be fitted to the data points
such that
where are unknown independent random errors with and , being a constant, then the method used is to calculate the estimates of the regression parameters by minimizing
If the errors do not have constant variance, i.e.,
then weighted least squares estimation is used in which
is minimized. For a more complete discussion of these least squares regression methods, and details of the mathematical techniques used, see Draper and Smith (1985) or Kendall and Stuart (1973).
| (6) |
| (7) |
 Computational methods for least squares regression
Computational methods for least squares regression
Let be the by matrix of independent variables and be the vector of values for the dependent variable. To find the least squares estimates of the vector of parameters, , the decomposition of is found, i.e.,
where , being a by upper triangular matrix, and an by orthogonal matrix. If is of full rank then is the solution to
where and is the first rows of . If is not of full rank, a solution is obtained by means of a singular value decomposition (SVD) of ,
where is a by diagonal matrix with nonzero diagonal elements, being the rank of , and and are by orthogonal matrices. This gives the solution
being the first columns of and being the first columns of .
This will be only one of the possible solutions. Other estimates may be obtained by applying constraints to the parameters. If weighted regression with a vector of weights is required then both and are premultiplied by .
The method described above will, in general, be more accurate than methods based on forming (), (or a scaled version), and then solving the equations
 Examining the fit of the model
Examining the fit of the model
Having fitted a model two questions need to be asked: first, ‘are all the terms in the model needed?’ and second, ‘is there some systematic lack of fit?’. To answer the first question either confidence intervals can be computed for the parameters or -tests can be calculated to test hypotheses about the regression parameters – for example, whether the value of the parameter, , is significantly different from a specified value, (often zero). If the estimate of is and its standard error is then the -statistic is
It should be noted that both the tests and the confidence intervals may not be independent. Alternatively -tests based on the residual sums of squares for different models can also be used to test the significance of terms in the model. If model , giving residual sum of squares with degrees of freedom , is a sub-model of model , giving residual sum of squares with degrees of freedom , i.e., all terms in model are also in model , then to test if the extra terms in model are needed the -statistic
may be used. These tests and confidence intervals require the additional assumption that the errors, , are Normally distributed.
To check for systematic lack of fit the residuals, , where is the fitted value, should be examined. If the model is correct then they should be random with no discernible pattern. Due to the way they are calculated the residuals do not have constant variance. Now the vector of fitted values can be written as a linear combination of the vector of observations of the dependent variable, , . The variance-covariance matrix of the residuals is then , being the identity matrix. The diagonal elements of , , can therefore be used to standardize the residuals. The are a measure of the effect of the th observation on the fitted model and are sometimes known as leverages.
If the observations were taken serially the residuals may also be used to test the assumption of the independence of the and hence the independence of the observations.
 Ridge regression
Ridge regression
When data on predictor variables are multicollinear, ridge regression models provide an alternative to variable selection in the multiple regression model. In the ridge regression case, parameter estimates in the linear model are found by penalised least squares:
where the value of the ridge parameter controls the trade-off between the goodness-of-fit and smoothness of a solution.
 Robust Estimation
Robust Estimation
Least squares regression can be greatly affected by a small number of unusual, atypical, or extreme observations. To protect against such occurrences, robust regression methods have been developed. These methods aim to give less weight to an observation which seems to be out of line with the rest of the data given the model under consideration. That is to seek to bound the influence. For a discussion of influence in regression, see Hampel et al. (1986) and Huber (1981).
There are two ways in which an observation for a regression model can be considered atypical. The values of the independent variables for the observation may be atypical or the residual from the model may be large.
The first problem of atypical values of the independent variables can be tackled by calculating weights for each observation which reflect how atypical it is, i.e., a strongly atypical observation would have a low weight. There are several ways of finding suitable weights; some are discussed in Hampel et al. (1986).
The second problem is tackled by bounding the contribution of the individual to the criterion to be minimized. When minimizing (7) a set of linear equations is formed, the solution of which gives the least squares estimates. The equations are
These equations are replaced by
| (8) |
where is the variance of the , and is a suitable function which down weights large values of the standardized residuals . There are several suggested forms for , one of which is Huber's function,
| (9) |
The solution to (8) gives the -estimates of the regression coefficients. The weights can be included in (8) to protect against both types of extreme value. The parameter can be estimated by the median absolute deviations of the residuals or as a solution to, in the unweighted case,
where is a suitable function and is a constant chosen to make the estimate unbiased. is often chosen to be where is given in (9). Another form of robust regression is to minimize the sum of absolute deviations, i.e.,
For details of robust regression, see Hampel et al. (1986) and Huber (1981).
Robust regressions using least absolute deviations can be computed using methods in E02 class.
 Generalized Linear Models
Generalized Linear Models
Generalized linear models are an extension of the general linear regression model discussed above. They allow a wide range of models to be fitted. These included certain nonlinear regression models, logistic and probit regression models for binary data, and log-linear models for contingency tables. A generalized linear model consists of three basic components:
| (a) | A suitable distribution for the dependent variable . The following distributions are common:
In addition to the obvious uses of models with these distributions it should be noted that the Poisson distribution can be used in the analysis of contingency tables while the gamma distribution can be used to model variance components. The effect of the choice of the distribution is to define the relationship between the expected value of , , and its variance and so a generalized linear model with one of the above distributions may be used in a wider context when that relationship holds. |
||||||||||||||||||||||||||||||
| (b) | A linear model , is known as a linear predictor. | ||||||||||||||||||||||||||||||
| (c) | A link function between the expected value of and the linear predictor, . The following link functions are available:
For the binomial distribution , observing out of :
For the Normal, Poisson, and gamma distributions:
For each distribution there is a canonical link. For the canonical link there exist sufficient statistics for the parameters. The canonical links are:
For the general linear regression model described above the three components are:
|
The model is fitted by maximum likelihood; this is equivalent to least squares in the case of the Normal distribution. The residual sums of squares used in regression models is generalized to the concept of deviance. The deviance is the logarithm of the ratio of the likelihood of the model to the full model in which , where is the estimated value of . For the Normal distribution the deviance is the residual sum of squares. Except for the case of the Normal distribution with the identity link, the and -tests based on the deviance are only approximate; also the estimates of the parameters will only be approximately Normally distributed. Thus only approximate - or -tests may be performed on the parameter values and approximate confidence intervals computed.
The estimates are found by using an iterative weighted least squares procedure. This is equivalent to the Fisher scoring method in which the Hessian matrix used in the Newton–Raphson method is replaced by its expected value. In the case of canonical links the Fisher scoring method and the Newton–Raphson method are identical. Starting values for the iterative procedure are obtained by replacing the by in the appropriate equations.
 Linear Mixed Effects Regression
Linear Mixed Effects Regression
In a standard linear model the independent (or explanatory) variables are assumed to take the same set of values for all units in the population of interest. This type of variable is called fixed. In contrast, an independent variable that fluctuates over the different units is said to be random. Modelling a variable as fixed allows conclusions to be drawn only about the particular set of values observed. Modelling a variable as random allows the results to be generalized to the different levels that may have been observed. In general, if the effects of the levels of a variable are thought of as being drawn from a probability distribution of such effects then the variable is random. If the levels are not a sample of possible levels then the variable is fixed. In practice many qualitative variables can be considered as having fixed effects and most blocking, sampling design, control and repeated measures as having random effects.
In a general linear regression model, defined by
there are fixed effects (the ) and a single random effect (the error term ).
| where | is a vector of observations on the dependent variable, |
| is an by design matrix of independent variables, | |
| is a vector of unknown parameters, | |
| and | is a vector of , independent and identically distributed, unknown errors, with , |
An extension to the general linear regression model that allows for additional random effects is the linear mixed effects regression model, (sometimes called the variance components model). One parameterisation of a linear mixed effects model is
and and are normally distributed with expectation zero and variance / covariance matrix defined by
| where | is a vector of observations on the dependent variable, |
| is an by design matrix of fixed independent variables, | |
| is a vector of unknown fixed effects, | |
| is an by design matrix of random independent variables, | |
| is a vector of length of unknown random effects, | |
| is a vector of length of unknown random errors, |
The methods currently available in this chapter are restricted to cases where
,
is the identity matrix and is a diagonal matrix. Given this restriction the random variables, , can be subdivided into groups containing one or more variables. The variables in the th group are identically distributed with expectation zero and variance . The model therefore contains three sets of unknowns, the fixed effects, , the random effects, , and a vector of variance components, , with . Rather than work directly with and the full likelihood function, is replaced by and the profiled likelihood function is used instead.
The model parameters are estimated using an iterative method based on maximizing either the restricted (profiled) likelihood function or the (profiled) likelihood functions. Fitting the model via restricted maximum likelihood involves maximizing the function
Whereas fitting the model via maximum likelihood involves maximizing
In both cases
Once the final estimates for have been obtained, the value of is given by
Case weights, , can be incorporated into the model by replacing and with and respectively, for a diagonal weight matrix .
 Quantile Regression
Quantile Regression
Quantile regression is related to least squares regression in that both are interested in studying the relationship between a response variable and one or more independent or explanatory variables. However, whereas least squares regression is concerned with modelling the conditional mean of the dependent variable, quantile regression models the conditional th quantile of the dependent variable, for some value of . So, for example, would be the median.
Throughout this section we will be making use of the following definitions:
| (a) | If is a real valued random variable with distribution function and density function , such that
|
||||
| (b) | denotes an indicator function taking the value if the logical expression is true and 0 otherwise, e.g., if and if . | ||||
| (c) | denotes a vector of observations on the dependent (or response) variable, . | ||||
| (d) | denotes an matrix of explanatory or independent variables, often referred to as the design matrix, and denotes a column vector of length which holds the th row of . |
 Finding a sample quantile as an optimization problem
Finding a sample quantile as an optimization problem
Consider the piecewise linear loss function
The minimum of the expectation
can be obtained by using the integral rule of Leibnitz to differentiate with respect to and then setting the result to zero, giving
hence
when the solution is unique. If the solution is not unique then there exists a range of quantiles, each of which is equally valid. Taking the smallest value of such a range ensures that the empirical quantile function is left-continuous. Therefore obtaining the th quantile of a distribution can be achieved by minimizing the expected value of the loss function .
This idea of obtaining the quantile by solving an optimization problem can be extended to finding the th sample quantile. Given a vector of observed values, , from some distribution the empirical distribution function, provides an estimate of the unknown distribution function giving an expected loss of
and therefore the problem of finding the th sample quantile, , can be expressed as finding the solution to the problem
effectively replacing the operation of sorting, usually required when obtaining a sample quantile, with an optimization.
 From least squares to quantile regression
From least squares to quantile regression
Given the vector it is a well known result that the sample mean, , solves the least squares problem
This result leads to least squares regression where, given design matrix and defining the conditional mean of as , an estimate of is obtained from the solution to
Quantile regression can be derived in a similar manner by specifying the th conditional quantile as and estimating as the solution to
| (10) |
 Quantile regression as a linear programming problem
Quantile regression as a linear programming problem
By introducing slack variables, and , the quantile regression minimization problem, (10), can be expressed as a linear programming (LP) problem, with primal and associated dual formulations
| (a) | Primal form
If denotes the th residual, , then the slack variables, , can be thought as corresponding to the absolute value of the positive and negative residuals respectively with
|
||||
| (b) | Dual form
The dual formulation of (11) is given by
|
||||
| (c) | Canonical form
Linear programming problems are often described in a standard way, called the canonical form. The canonical form of an LP problem is
Letting denote a vector of zeros denote a vector of arbitarily small or large values, denote the identity matrix, denote the row vector constructed by concatenating the elements of vector to the elements of vector and denote the matrix constructed by concatenating the columns of matrix onto the columns of matrix then setting
|
Once expressed as an LP problem the parameter estimates can be obtained in a number of ways, for example via the inertia-controlling method of Gill and Murray (1978) (see e04mf), the simplex method or an interior point method as used by g02qf and g02qg.
 Estimation of the covariance matrix
Estimation of the covariance matrix
Koenker (2005) shows that the limiting covariance matrix of
is of the form of a Huber Sandwich. Therefore, under the assumption of Normally distributed errors
where
and
denotes the conditional density of the response evaluated at the th conditional quantile.
| (13) |
More generally, the asymptotic covariance matrix for
has blocks defined by
| (14) |
Under the assumption of independent, identically distributed (iid) errors, (13) simplifies to
where is the sparsity function, given by
a similar simplification occurs with (14).
In cases where the assumption of iid errors does not hold, Powell (1991) suggests using a kernel estimator of the form
for some bandwidth parameter satisfying and and Hendricks and Koenker (1991) suggest a method based on an extension of the idea of sparsity.
Rather than use an asymptotic estimate of the covariance matrix, it is also possible to use bootstrapping. Roughly speaking the original data is resampled and a set of parameter estimates obtained from each new sample. A sample covariance matrix is then constructed from the resulting matrix of parameter estimates.
 Latent Variable Methods
Latent Variable Methods
Regression by means of projections to latent structures also known as partial least squares, is a latent variable linear model suited to data for which:
- the number of -variables is high compared to the number of observations;
- -variables and/or -variables are multicollinear.
Latent variables are linear combinations of -variables that explain variance in and -variables. These latent variables, known as factors, are extracted iteratively from the data. A choice of the number of factors to include in a model can be made by considering diagnostic statistics such as the variable influence on projections (VIP).
 Recommendations on Choice and Use of Available Methods
Recommendations on Choice and Use of Available Methods
 Correlation
Correlation
 Product-moment correlation
Product-moment correlation
Let be the sum of squares of deviations from the mean, , for the variable for a sample of size , i.e.,
and let be the cross-products of deviations from the means, and , for the variables and for a sample of size , i.e.,
Then the sample covariance of and is
and the product-moment correlation coefficient is
g02ba computes the product-moment correlation coefficients.
g02bt updates the sample sums of squares and cross-products and deviations from the means by the addition/deletion of a (weighted) observation.
g02bu computes the sample sums of squares and cross-products deviations from the means (optionally weighted). The output from multiple calls to g02bu can be combined via a call to (G02BZF not in this release), allowing large datasets to be summarised across multiple processing units.
g02bt updates the sample sums of squares and cross-products and deviations from the means by the addition/deletion of a (weighted) observation.
g02bw computes the product-moment correlation coefficients from the sample sums of squares and cross-products of deviations from the means.
The three methods compute only the upper triangle of the correlation matrix which is stored in a one-dimensional array in packed form.
g02bx computes both the (optionally weighted) covariance matrix and the (optionally weighted) correlation matrix. These are returned in two-dimensional arrays. (Note that g02bt and g02bu can be used to compute the sums of squares from zero.)
g02bg can be used to calculate the correlation coefficients for a subset of variables in the data matrix.
 Product-moment correlation with missing values
Product-moment correlation with missing values
If there are missing values then g02bu and g02bx, as described above, will allow casewise deletion by you giving the observation zero weight (compared with unit weight for an otherwise unweighted computation).
Other methods also handle missing values in the calculation of unweighted product-moment correlation coefficients. Casewise exclusion of missing values is provided by g02bb while pairwise omission of missing values is carried out by g02bc. These two methods calculate a correlation matrix for all the variables in the data matrix; similar output but for only a selected subset of variables is provided by methods g02bh and g02bj respectively. As well as providing the Pearson product-moment correlation coefficients, these methods also calculate the means and standard deviations of the variables, and the matrix of sums of squares and cross-products of deviations from the means. For all four methods you are free to select appropriate values for consideration as missing values, bearing in mind the nature of the data and the possible range of valid values. The missing values for each variable may be either different or alike and it is not necessary to specify missing values for all the variables.
 Nonparametric correlation
Nonparametric correlation
There are five methods which perform nonparametric correlations, each of which is capable of producing both Spearman's rank order and Kendall's tau correlation coefficients. The basic underlying concept of both these methods is to replace each observation by its corresponding rank or order within the observations on that variable, and the correlations are then calculated using these ranks.
It is obviously more convenient to order the observations and calculate the ranks for a particular variable just once, and to store these ranks for subsequent use in calculating all coefficients involving that variable; this does however require an amount of store of the same size as the original data matrix, which in some cases might be excessive. Accordingly, some methods calculate the ranks only once, and replace the input data matrix by the matrix of ranks, which are then also made available to you on exit from the method, while others preserve the data matrix and calculate the ranks a number of times within the method; the ranks of the observations are not provided as output by methods which work in the latter way. If it is possible to arrange the program in such a way that the first technique can be used, then efficiency of timing is achieved with no additional storage, whereas in the second case, it is necessary to have a second matrix of the same size as the data matrix, which may not be acceptable in certain circumstances; in this case it is necessary to reach a compromise between efficiency of time and of storage, and this may well be dependent upon local conditions.
Methods g02bn and g02bq both calculate Kendall's tau and/or Spearman's rank order correlation coefficients taking no account of missing values; g02bn does so by calculating the ranks of each variable only once, and replacing the data matrix by the matrix of ranks, whereas g02bq calculates the ranks of each variable several times. Methods g02bp and g02br provide the same output, but treat missing values in a ‘casewise’ manner (see above); g02bp calculates the ranks of each variable only once, and overwrites the data matrix of ranks, while g02br determines the ranks of each variable several times. For ‘pairwise’ omission of missing data (see above), the method g02bs provides Kendall and/or Spearman coefficients.
Since g02bn and g02bp order the observations and calculate the ranks of each variable only once, then if there are variables involved, there are only separate ‘ranking’ operations; this should be contrasted with the method used by methods g02bq and g02br which perform similar ranking operations. These ranking operations are by far the most time-consuming parts of these nonparametric methods, so for a matrix of as few as five variables, the time taken by one of the slower methods can be expected to be at least a factor of two slower than the corresponding efficient method; as the number of variables increases, so this relative efficiency factor increases. Only one method, g02bs, is provided for pairwise missing values, and this method carries out separate rankings; since by the very nature of the pairwise method it is necessary to treat each pair of variables separately and rank them individually, it is impossible to reduce this number of operations, and so no alternative method is provided.
 Partial correlation
Partial correlation
 Robust correlation
Robust correlation
g02hl and g02hm compute robust estimates of the variance-covariance matrix by solving the equations
and
as described in [Robust estimation of correlation coefficients] for user-supplied functions and . Two options are available for , either for all or .
In general g02hl will be considerably faster than g02hm and should be used if derivatives are available.
g02hk computes a robust variance-covariance matrix for the following functions:
and
for constants , and .
These functions solve a minimax space problem considered by Huber (1981). The values of , and are calculated from the fraction of gross errors; see Hampel et al. (1986) and Huber (1981).
To compute a correlation matrix from the variance-covariance matrix g02bw may be used.
 Nearest correlation matrix
Nearest correlation matrix
Four methods are provided to calculate a nearest correlation matrix. The choice of method will depend on what definition of ‘nearest’ is required and whether there is any particular structure desired in the resulting correlation matrix.
g02aa computes the nearest correlation matrix in the Frobenius norm, using the method of Qi and Sun (2006).
g02ab uses an extension of the method implemented in g02aa allowing for the row and column weighted Frobenius norm to be used as well as bounds on the eigenvalues of the resulting correlation matrix to be specified.
g02ae computes the factor loading matrix, allowing a correlation matrix with a -factor structure to be computed.
(G02AJF not in this release) again computes the nearest correlation matrix in the Frobenius norm, but allows for element-wise weighting as well as bounds on the eigenvalues.
 Regression
Regression
 Simple linear regression
Simple linear regression
Four methods are provided for simple linear regressions: g02ca and g02cc perform the simple linear regression with a constant term (equation (1) above), while g02cb and g02cd fit the simple linear regression with no constant term (equation (2) above). Two of these methods, g02cc and g02cd, take account of missing values, which the others do not. In these two methods, an observation is omitted if it contains a missing value for either the dependent or the independent variable; this is equivalent to both the casewise and pairwise methods, since both are identical when there are only two variables involved. Input to these methods consists of the raw data, and output includes the coefficients, their standard errors and values for testing the significance of the coefficients; the value for testing the overall significance of the regression is also given.
 Ridge regression
Ridge regression
g02ka calculates a ridge regression, optimizing the ridge parameter according to one of four prediction error criteria.
g02kb calculates ridge regressions for a given set of ridge parameters.
 Polynomial regression and nonlinear regression
Polynomial regression and nonlinear regression
No methods are currently provided in this chapter for polynomial regression. If you wish to perform polynomial regressions you have three alternatives: you can use the multiple linear regression methods, g02da, with a set of independent variables which are in fact simply the same single variable raised to different powers, or you can use the method (G04EAF not in this release) to compute orthogonal polynomials which can then be used with g02da, or you can use the methods in E02 class (Curve and Surface Fitting) which fit polynomials to sets of data points using the techniques of orthogonal polynomials. This latter course is to be preferred, since it is more efficient and liable to be more accurate, but in some cases more statistical information may be required than is provided by those methods, and it may be necessary to use the methods of this chapter.
More general nonlinear regression models may be fitted using the optimization methods in E04 class, which contains methods to minimize the function
where the regression parameters are the variables of the minimization problem.
 Multiple linear regression – general linear model
Multiple linear regression – general linear model
g02da fits a general linear regression model using the method and an SVD if the model is not of full rank. The results returned include: residual sum of squares, parameter estimates, their standard errors and variance-covariance matrix, residuals and leverages. There are also several methods to modify the model fitted by g02da and to aid in the interpretation of the model.
g02dc adds or deletes an observation from the model.
g02dd computes the parameter estimates, and their standard errors and variance-covariance matrix for a model that is modified by g02dc, g02de or g02df.
g02de adds a new variable to a model.
g02df drops a variable from a model.
g02dg fits the regression to a new dependent variable, i.e., keeping the same independent variables.
g02dk calculates the estimates of the parameters for a given set of constraints, (e.g., parameters for the levels of a factor sum to zero) for a model which is not of full rank and the SVD has been used.
g02dn calculates the estimate of an estimable function and its standard error.
Note: g02de also allows you to initialize a model building process and then to build up the model by adding variables one at a time.
If you wish to use methods based on forming the cross-products/correlation matrix (i.e., () matrix) rather than the recommended use of g02da then the following methods should be used.
For regression through the origin (i.e., no constant) g02ch preceded by:
For regression with intercept (i.e., with constant) g02cg preceded by:
Note that the four methods using pairwise deletion of missing value (marked with ) should be used with great caution as the use of this method can lead to misleading results, particularly if a significant proportion of values are missing.
Both g02cg and g02ch require that the correlations/sums of squares involving the dependent variable must appear as the last row/column. Because the layout of the variables in your data array may not be arranged in this way, two methods, g02ce and g02cf, are provided for rearranging the rows and columns of vectors and matrices. g02cf simply reorders the rows and columns while g02ce forms smaller vectors and matrices from larger ones.
 Selecting regression models
Selecting regression models
To aid the selection of a regression model the following methods are available.
(G02EAF not in this release) computes the residual sums of squares for all possible regressions for a given set of dependent variables. The method allows some variables to be forced into all regressions.
(G02ECF not in this release) computes the values of and from the residual sums of squares as provided by (G02EAF not in this release).
(G02EEF not in this release) enables you to fit a model by forward selection. You may call (G02EEF not in this release) a number of times. At each call the method will calculate the changes in the residual sum of squares from adding each of the variables not already included in the model, select the variable which gives the largest change and then if the change in residual sum of squares meets the given criterion will add it to the model.
g02ef uses a full stepwise selection to choose a subset of the explanatory variables. The method repeatedly applies a forward selection step followed by a backward elimination step until neither step updates the current model.
 Residuals
Residuals
g02fa computes the following standardized residuals and measures of influence for the residuals and leverages produced by g02da:
| (i) | Internally studentized residual; |
| (ii) | Externally studentized residual; |
| (iii) | Cook's statistic; |
| (iv) | Atkinson's statistic. |
g02fc computes the Durbin–Watson test statistic and bounds for its significance to test for serial correlation in the errors, .
 Robust regression
Robust regression
For robust regression using -estimates instead of least squares the method g02ha will generally be suitable. g02ha provides a choice of four -functions (Huber's, Hampel's, Andrew's and Tukey's) plus two different weighting methods and the option not to use weights. If other weights or different -functions are needed the method g02hd may be used. g02hd requires you to supply weights, if required, and also methods to calculate the -function and, optionally, the -function. g02hb can be used in calculating suitable weights. The method g02hf can be used after a call to g02hd in order to calculate the variance-covariance estimate of the estimated regression coefficients.
For robust regression, using least absolute deviation, (E02GAF not in this release) can be used.
 Generalized linear models
Generalized linear models
There are four methods for fitting generalized linear models. The output includes: the deviance, parameter estimates and their standard errors, fitted values, residuals and leverages.
g02ga Normal distribution.
g02gb binomial distribution.
g02gc Poisson distribution.
g02gd gamma distribution.
While g02ga can be used to fit linear regression models (i.e., by using an identity link) this is not recommended as g02da will fit these models more efficiently. g02gc can be used to fit log-linear models to contingency tables.
In addition to the methods to fit the models there is one method to predict from the fitted model and two methods to aid interpretation when the fitted model is not of full rank, i.e., aliasing is present.
g02gp computes a predicted value and its associated standard error based on a previously fitted generalized linear model.
g02gk computes parameter estimates for a set of constraints, (e.g., sum of effects for a factor is zero), from the SVD solution provided by the fitting method.
g02gn calculates an estimate of an estimable function along with its standard error.
 Linear mixed effects regression
Linear mixed effects regression
There are four methods for fitting linear mixed effects regression.
g02ja (G02JDF not in this release) uses restricted maximum likelihood (REML) to fit the model.
g02jb (G02JEF not in this release) uses maximum likelihood to fit the model.
For all methods the output includes: either the maximum likelihood or restricted maximum likelihood and the fixed and random parameter estimates, along with their standard errors. Whilst it is possible to fit a hierachical model using g02ja or g02jb, (G02JDF not in this release) (G02JEF not in this release) allow the model to be specified in a more intuitive way. (G02JCF not in this release) must be called prior to calling (G02JDF not in this release) (G02JEF not in this release).
As the estimates of the variance components are found using an iterative procedure initial values must be supplied for each . In all four methods you can either specify these initial values, or allow the method to calculate them from the data using minimum variance quadratic unbiased estimation (MIVQUE0). Setting the maximum number of iterations to zero in any of the methods will return the corresponding likelihood, parameter estimates and standard errors based on these initial values.
 Linear quantile regression
Linear quantile regression
Two methods are provided for performing linear quantile regression, g02qf and g02qg. Of these, g02qf provides a simplified interface to g02qg, where many of the input parameters have been given default values and the amount of output available has been reduced.
Prior to calling g02qg the optional parameter array must be initialized by calling (G02ZKF not in this release) with optstr set to initialize. Once these arrays have been initialized (G02ZLF not in this release) can be called to query the value of an optional parameter.
 Partial Least Squares (PLS)
Partial Least Squares (PLS)
 References
References
Atkinson A C (1986) Plots, Transformations and Regressions Clarendon Press, Oxford
Churchman C W and Ratoosh P (1959) Measurement Definitions and Theory Wiley
Cook R D and Weisberg S (1982) Residuals and Influence in Regression Chapman and Hall
Draper N R and Smith H (1985) Applied Regression Analysis (2nd Edition) Wiley
Gill P E and Murray W (1978) Numerically stable methods for quadratic programming Math. Programming 14 349–372
Hammarling S (1985) The singular value decomposition in multivariate statistics SIGNUM Newsl. 20(3) 2–25
Hampel F R, Ronchetti E M, Rousseeuw P J and Stahel W A (1986) Robust Statistics. The Approach Based on Influence Functions Wiley
Hays W L (1970) Statistics Holt, Rinehart and Winston
Hendricks W and Koenker R (1991) Hierarchical spline models for conditional quantiles and the demand for electricity Journal of the Maerican Statistical Association 87 58–68
Huber P J (1981) Robust Statistics Wiley
Kendall M G and Stuart A (1973) The Advanced Theory of Statistics (Volume 2) (3rd Edition) Griffin
Koenker R (2005) Quantile Regression Econometric Society Monographs, Cambridge University Press, New York
McCullagh P and Nelder J A (1983) Generalized Linear Models Chapman and Hall
Powell J L (1991) Estimation of monotonic regression models under quantile restrictions Nonparametric and Semiparametric Methods in Econometrics Cambridge University Press, Cambridge
Qi H and Sun D (2006) A quadratically convergent Newton method for computing the nearest correlation matrix SIAM J. Matrix AnalAppl 29(2) 360–385
Searle S R (1971) Linear Models Wiley
Siegel S (1956) Non-parametric Statistics for the Behavioral Sciences McGraw–Hill
Weisberg S (1985) Applied Linear Regression Wiley